[l,r] 구간에서 서로 다른 수의 갯수를 세는 쿼리는 보통 offline 하게 mo's algorithm 등을 사용하여 해결하는데, online한 쿼리를 강제하는 문제에서는 보통 persistant segment tree를 깔끔한 정해로 보는 것 같습니다.
입력값을 조금 처리하는 것으로, merge sort tree를 통해서 이러한 쿼리를 처리할 수 있기 때문에, 이에 대해서 짚어보도록 하겠습니다.
Merge Sort Tree
세그먼트 트리와 비슷하게 이진 트리에 값을 저장하는데,
세그먼트트리는 구간을 대표하는 어떤 값들을 저장한다면 MST는 구간 그 자체를 merge해놓은 형태를 저장합니다. 이 과정이 마치 Merge Sort의 중간 과정을 모두 저장해놓은 형태와 비슷하기에 머지 소트 트리라고 부르며, 머지소트 트리의 각 노드 역시도 정렬된 배열의 형태라는 특징이 있습니다.
주로 구간에 대한 쿼리를 처리하고픈데, 구간 전체를 반드시 들고 있어야 할 때에 사용하며,
- [l,r] 에서의 K번째 수 - boj 7469
- [l,r] 에서 K보다 큰/작은 수의 개수 - boj 13544
등등의 문제에 활용할 수 있습니다. 둘 모두 기본적으로 구간 내의 원소를 모두 들고 있어야 계산할 수 있는 쿼리들입니다.
14898 서로 다른 수와 쿼리 2
단순히 보면 MST에서 unique한 값만 남기고 있으면 되지 않나 싶지만, 이 경우 vector의 복사와 할당에 의해 TLE를 받을 확률이 높습니다.
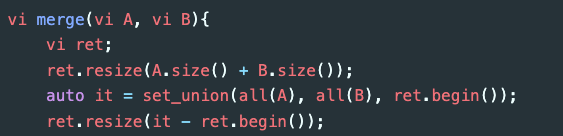
바로 윗 풀이에서는 std::merge 대신 std::set_union 함수를 사용하였는데, 이 경우 TLE를 받는것을 확인할 수 있습니다.
애초에 vector<int> 를 매개변수로 넘겨주는 시점에서 메모리 소모 또한 굉장히 많은 편인데, 이 문제를 다른 방법으로 해결할 수 있을까요?
"모종의 방법" 으로 숫자가 같은, 중복되는 수를 쿼리 내에 포함하지 않을 방법이 있다면 이 문제를 해결할 수 있게 됩니다.
MST로 문제를 해결하기
전처리
쿼리를 해결하기 위해서, 우리는 구간 내에서 중복되는 값을 제거할 방법을 찾아야 합니다. 즉, 구간 내의 배열에 대해서 겹치는 수가 있을 경우, 그것들 중 한 개만 선택할 방법을 만들어야 합니다.
편의상 중복되는 수에 대해서 왼쪽 끝이나 오른쪽 끝 하나만 세는 것이 편할 것이고, 이 중에서는 왼쪽 끝 하나만 세는 케이스를 고민해보도록 하겠습니다.
왼쪽 끝이 아닌 다른 모든 숫자들을 구간에 포함시키지 않기 위해서는, 왼쯕 끝이 있는지를 알아볼 수 있게 하는 것이 급선무일 것입니다.
입력받은 값 a[i]로 prv[i]를 제작, prv[i]는
- a[i]가 앞서 등장한 적이 있는 경우 앞선 a[i]의 인덱스,
- a[i]가 등장한 적이 없는 경우 0 (0-based-index 의 경우 -1)
로 구성합니다.
이제 자기 자신이 왼쪽 끝인 경우는 prv[i]가 0인지를 통해 알아볼 수 있습니다.
0의 갯수를 세는 segment tree를 구성해주면 전체 구간에서 한번만 등장했던 수들의 갯수를 세줄 수 있게 됩니다. 하지만 이것은 의도했던 풀이가 아니군요.
prv[i]에 대한 고민
자기 자신이 왼쪽 끝이 아니면서, 부분 구간에서의 왼쪽 끝인 수 K를 생각해 보겠습니다. 이 경우 prv[i] 의 값은 부분 구간[l,r] 에서 l보다 작은 어딘가를 가리키고 있습니다.
다른 모든 K와 값이 같은 수 K'의 prv[i'] 는 못해도 K의 인덱스 i보다는 크거나 같은데, K와 K'들이 구간 [l,r] 에 속해있다는 제약사항으로 인해
l <= i' <= r 이라는 조건을 충족하게 됩니다.
즉, 구간에 있는 수 prv[i] 들에 대해서 두번 이상 등장하는 경우 모두 [l,r] 구간 안에 있음을 알아낼 수 있고,
보다 간단하게 정리하자면 prv[i] 가 [l,inf] 구간 안에 포함되는 경우 i번째 수 a[i]는 구간 내에서 중복되는 수 임을 알아낼 수 있게 됩니다.
이제 중복되지 않는 수들은 [-inf,l) 구간에 있음을 확인할 수 있으며, 이 구간에 속하는 수의 갯수를 셀 수 있는 segment tree를 구성하면 이 문제를 쿼리당 O(logN)에 해결할 수 있게 됩니다.
머지소트트리
- [l,r] 에서 K보다 큰/작은 수의 개수 - boj 13544
의 아이디어를 차용해서, 각 입력값 a[i] 에 대해서 prv[i] 배열을 만듭니다.
만들어진 prv[i] 배열로 MST를 구성하고,
MST 내에서 K보다 작은 수의 갯수를 세는 쿼리를 std::lower_bound 등을 통해 만들면 이 문제를 해결할 수 있습니다.
이러한 풀이에 대해 잘 정리된 글이 있어 첨부합니다.

영문 본문에서는 prv[i]가 아니라 보다 큰 인덱스를 가리키는 nxt[i] 배열을 만들어서 구성하였는데, prv[i] 배열 처리로도 이 문제를 해결할 수 있으며 이 경우 입력과 동시에 prv[i] 배열을 구성하고 MST에 넣어주는 것까지 가능하므로 보다 편리합니다.
prv[i]를 구성할때 이전에 등장하였는지의 여부는 unordered_map<int,int>을 사용하면 편리합니다
for(int i=1; i<=N; i++){
cin >> K;
if(chk.find(K) == chk.end()) prv[i] = 0;
else prv[i] = chk[K];
chk[K] = i;
seg[i+M-1].push_back(prv[i]);
}배열 a[i]를 입력받아 prv[i]를 구성하고 MST에 넣어주는 부분입니다.
void init(){
for(int i=M-1; i; i--){
seg[i].resize(seg[i*2].size() + seg[i*2+1].size());
merge(all(seg[i*2]), all(seg[i*2+1]), seg[i].begin());
}
}입력받은 이후 init() 함수를 실행시켜 MST를 완성하면, 쿼리를 날릴 수 있게 됩니다.