2024-01-23 • 8 min read

cpp[8] - 함수

본격적으로 복잡한 프로그램을 작성할 때에는, 수많은 계산을 처리하게 되는데, 그것을 전부 메인함수 안에 적어넣었다가는 가독성이 심각하게 떨어집니다.

원하는 기능별로 블록으로 묶어낼 수 있게 해주는 함수를 알아보겠습니다.

수학에서의 함수

고등수학에서의 함수의 정의는 아래와 같습니다

두 집합 $X$, $Y$ 에 대하여
$X$의 각 원소에 $Y$의 원소가 대응될 때 $f:X \rightarrow Y$ 이고,
$X$의 원소 $x$ 에 대해서 대응되는 $Y$의 원소가 $y$ 일때 $f(x) = y$ 이다.

하지만, 프로그래밍에서는 중학수학에서 봤던 정의를 사용하는것이 조금 더 잘 와닿습니다.

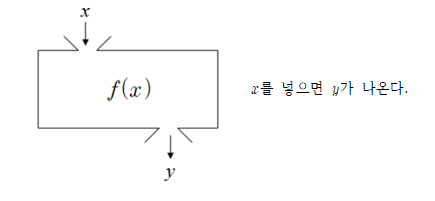
보통 이렇게 박스에 비유하는 것이 중학수학에서의 함수의 정의인데, 저 f(x) 안에 개발자가 원하는 어떤 수많은 연산을 거치고, 그 결과값이 y 혹은 출력 등으로 나옵니다.

함수의 정의

함수를 만드는 법은 아래와 같습니다

int f(int x){}
자료형 함수이름(변수){내용}

함수 안에서 return k; 문장을 사용할 수 있습니다.
return 문이 적힌 즉시 해당 블록의 실행을 멈추고, 그 뒤에 적힌 값을 마치 변수처럼 반환합니다.

즉,

int f(int x){ return x*2; }

cout << f(5);

f 함수가 위와 같은 상황에서 f(5) 를 호출하면, return문으로 받은 결과인 10을 출력하게 됩니다.

온 세상이 함수다

여기서 뭔가 눈치채신 점이 있다면, 지금까지 봐왔던 int main() 을 포함해서 생각보다 많은 곳에서 f(x) 와 비슷한 구문으로 프로그램을 실행하고 있다는 것입니다.

앞선 #include <iostream> 을 통해 불러온 수많은 기능들은 대부분이 함수로 구성되어 있으며, 저희는 C++ 언어를 개발한 사람들이 미리 만들어둔 함수를 통해서 화면 출력 등을 편하게 하고 있는 것입니다.

일반적으로 cin이라는 구문도 하나의 함수와 같아서,

struct stat buf;
fstat(0, &buf);
char *p = (char *)mmap(0, buf.st_size, PROT_READ, MAP_SHARED, 0, 0);

// readInt example
int t = *p++ & 15;
while (*p > 32) t = t * 10 + (*p++ & 15);

숫자를 입력받는 부분을 굳이 풀어서 쓰자면 이런 느낌으로 풀어서 작성할 수도 있습니다. 요거는 전혀 중요하지 않은 이야기니까 위에 소스코드는 어 그렇구나 하고 넘기셔도 되고,

중요한것은 cout, cin 같은 기본적인 구문들조차 전부 함수로 누군가가 만들어둔 것이라는 게 핵심입니다.

함수를 사용하는 이유

문제를 통해서 보도록 하겠습니다
대소문자 바꾸기 문제는 문자 그대로 입력된 문자열의 대소문자를 바꾸는 프로그램을 작성해야 합니다.

이를 앞선

의 개념만을 사용해서 풀어보면 아래와 같습니다.

#include <iostream>
using namespace std;

int main(){
	string s;
	cin >> s;

	for(int i=0; i<s.length(); i++){
		if('a' <= s[i] && s[i] <= 'z'){
			s[i] += 'A'-'a';
		}
		else if('A' <= s[i] && s[i] <= 'Z'){
			s[i] += 'a'-'A';
		}
	}
	cout << s;
	return 0;
}

이 소스코드에서 핵심인 부분은 대소문자를 바꾸는

if('a' <= s[i] && s[i] <= 'z'){
	s[i] += 'A'-'a';
}
else if('A' <= s[i] && s[i] <= 'Z'){
	s[i] += 'a'-'A';
}

입니다.
이 부분을 change() 라는 함수를 작성해서 분리해보도록 하겠습니다.

#include <iostream>
using namespace std;

char change(char c){
	if('a' <= c && c <= 'z'){
		return c + 'A'-'a';
	}
	else if('A' <= s[i] && s[i] <= 'Z'){
		return c + 'a'-'A';
	}
}

int main(){
	string s;
	cin >> s;

	for(int i=0; i<s.length(); i++){
		s[i] = change(s[i]);
	}
	cout << s;
	return 0;
}

이렇게 작성하니 메인 함수 안의 반복문이 의미하는 바가
모든 글자들에 대해서 대소문자 바꾸기 로 조금 더 명확해졌습니다.

이때 함수 change() 의 역할은 주어진 한 글자의 대소문자를 바꾼다 입니다.

어려운 문제를 통해 예제를 보겠습니다.

int ccw(pll A, pll B, pll C){
    ll ret = (A.x*B.y + B.x*C.y + C.x*A.y) - (A.y*B.x + B.y*C.x + C.y*A.x);
    if(ret>0) return 1;
    if(ret<0) return -1;
    return 0;
}

ll dist(pll A, pll B){
    ll X = (A.x-B.x);
    ll Y = (A.y-B.y);
    return X*X + Y*Y;
}

bool cross(pll A, pll B, pll C, pll D){
    int AB = ccw(A,B,C) * ccw(A,B,D);
    int CD = ccw(C,D,A) * ccw(C,D,B);

    if(AB == 0 && CD == 0){
        if(A>B) swap(A,B);
        if(C>D) swap(C,D);
        return C<=B && A<=D;
    }

    return AB<=0 && CD<=0;
}

vector<pll> convexHull(vector<pll> points){
    if(points.size() <= 1) return points;
    swap(points[0], *min_element(points.begin(), points.end()));

    sort(points.begin()+1, points.end(), [&](auto A, auto B){
        int dir = ccw(points[0], A, B);
        if(dir != 0) return dir > 0;
        return dist(points[0], A) < dist(points[0], B);
    });

    vector<pll> ret;
    for(auto p : points){
        while(ret.size() >=2 && ccw(ret[ret.size()-2], ret[ret.size()-1], p) <= 0) ret.pop_back();
        ret.push_back(p);
    }
    return ret;
}

boj 3878 점 분리 문제입니다.
문제에서 요구하고 있는 것이 많기 때문에, 함수를 4개정도 만들어서 사용하고 있습니다.

cross() 함수를 작성하지 않고 선분의 겹침 판별을 직접 해주어도 되겠지만,
이렇게 함수를 사용하여 소스코드를 분리했음에도 140줄이 넘는 긴 소스코드를 작성해야만 했습니다.

cross() 함수 안에서도 ccw() 함수를 사용해서 프로그램의 길이를 줄여주고 있는 만큼, 이걸 반복문을 통해서 일일히 풀어 쓰게 된다면 논리를 이해하기에 너무나도 길고 장황한 프로그램이 나오게 됩니다.

결론

프로그램의 논리를 이해함에 있어서,

이만큼이 "어떤 것" 을 구하는 부분이구나

로 접근하는 것보다는 해당 부분을 함수로 묶어서

이 줄이 "어떤 것" 을 구하는 부분이구나

가 가독성 측면에서 한없이 좋아지기 때문에 함수로 묶는 것이고,
어려운 문제로 접근하실수록

이 함수는 어떤 역할을 하는가
이 함수의 실행 결과로 받은 값은 뭐의 결과인가
를 이해하시는게 소스코드를 작성할때 도움이 많이 됩니다.

지금까지 풀어보신 모든 문제를 함수로 묶을 수 있기 때문에, 딱히 꼭 풀어보아야 한다 하는 문제는 없으나,

문제를 해결하실 때 소스코드가 너무 길어지는거 같다고 판단하시면 함수로 묶어서 분리하는 연습을 해보시면 도움이 많이 될 것입니다.