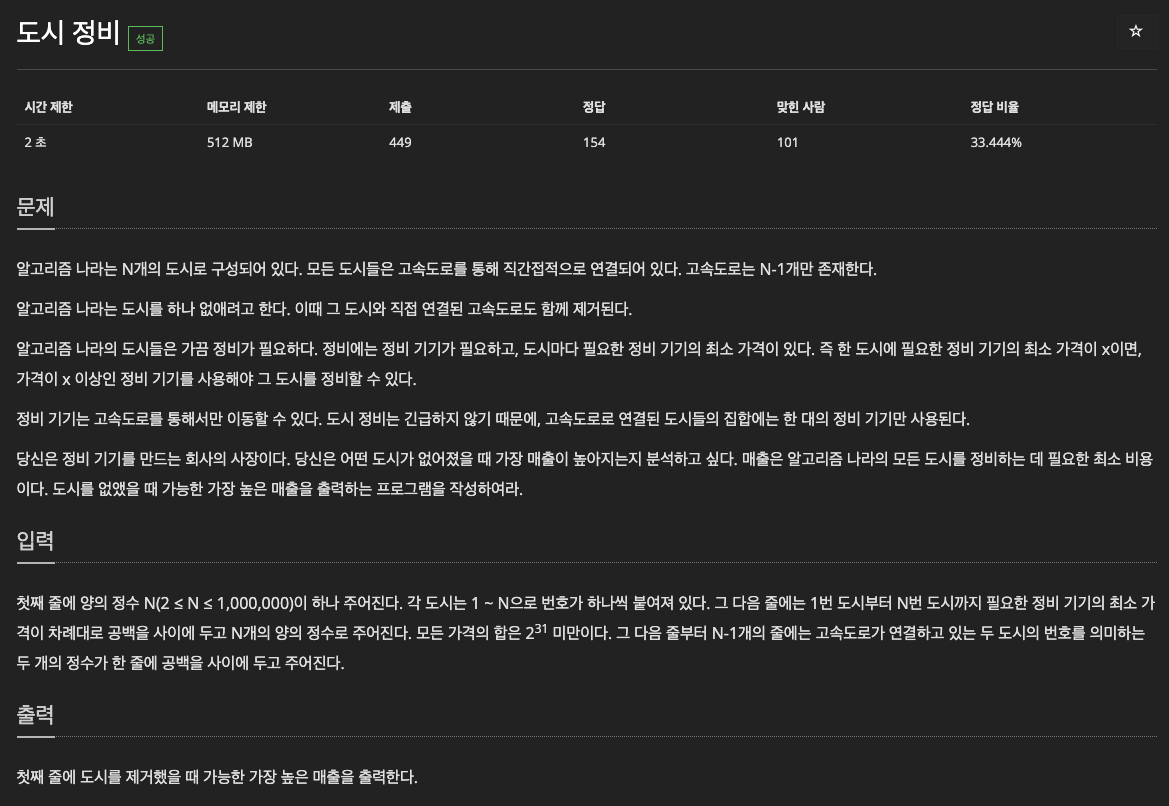
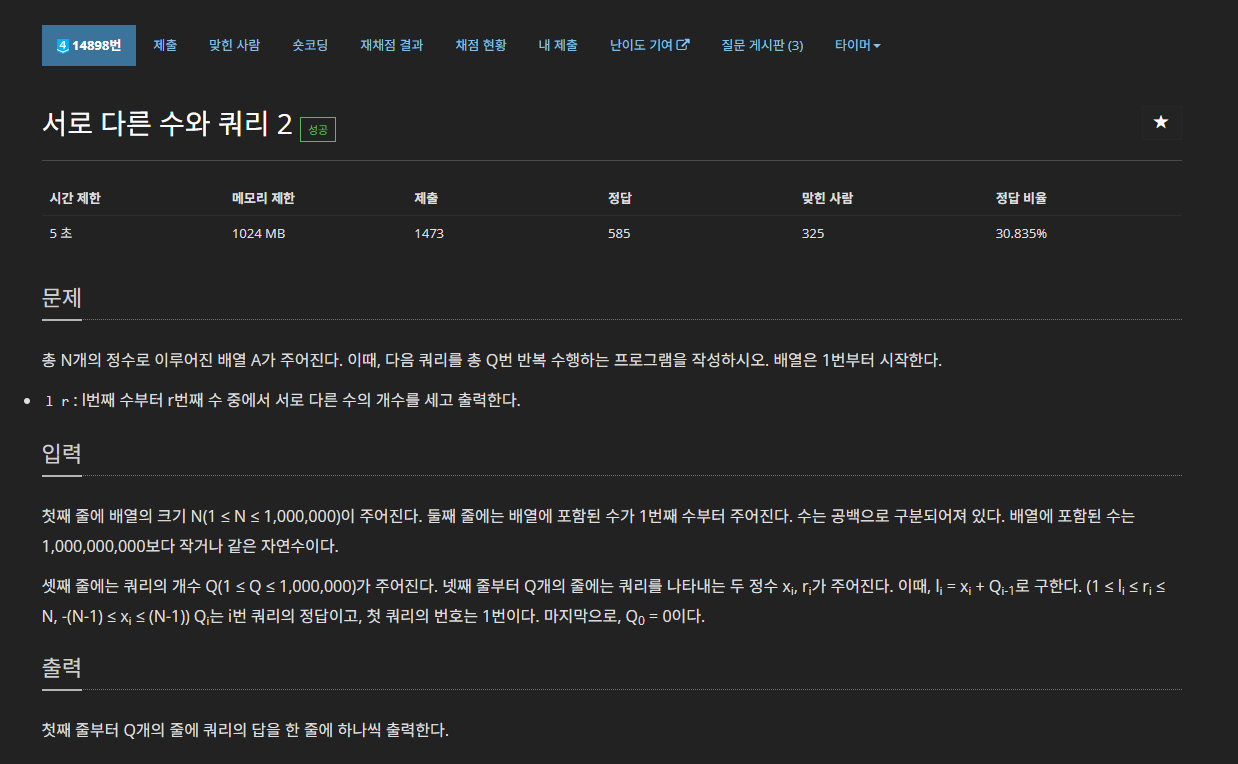
문제푸는데 간만에

오...

싶은 문제여서 가져와봤습니다. 2024 카카오 겨울 인턴십 기출문제인듯 합니다. indegree와 outdegree를 적절하게 활용해봅시다.

임의로 추가한 정점 구하기

임의로 추가한 정점이 가지는 가장 큰 특징은, indegree가 없다는 것입니다. 다시말해서, 임의로 추가한 정점 P에서 다른 정점으로 나가는 간선은 많지만, 정점 P로 가는 간선은 하나도 없습니다.

이 특징을 이용해서,

    for(auto k : edges){
        outdegree[k[0]]++;
        indegree[k[1]]++;
        
        g[k[0]].push_back(k[1]);
    }

를 통해 각 정점마다

• 다른 정점으로 나가는 간선의 갯수(outdegree)
• 다른 정점에서 들어오는 간선의 갯수(indegree)

를 세주고, 입력에서 들어왔던걸 인접리스트 형태로 변경시켜 줍니다.

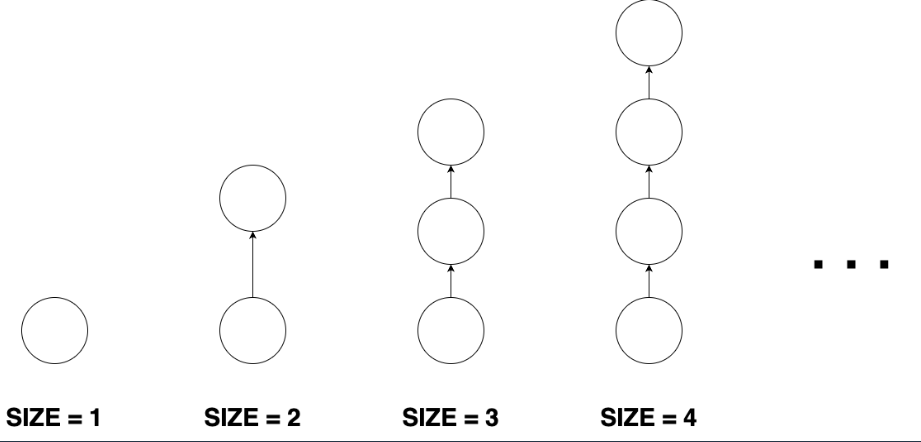
이때, 막대 모양 그래프의 시작점 역시 indegree가 없습니다. 따라서 indegree가 0일때 라는 조건만으로는 원하는 정점을 찾을 수 없으며, 문제 제한사항의

도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 수의 합은 2이상입니다.

라는 조건에 의거해 outdegree가 2 이상이 되기 때문에,

    for(int i=1; i<=1000000; i++){
        if(indegree[i] == 0 && outdegree[i] >= 2){ // 핵심 정점을 찾음.
            ans[0] = i;
            break;
        }
    }

를 통해 정점을 찾아줍니다.

그래프 구분하기

중심이 되는 정점을 찾았으면, 해당 정점과 연결된 모든 그래프들은

• 도넛 모양 그래프
• 막대 모양 그래프
• 8자 모양 그래프

로 나뉘게 됩니다.

이 셋 중 가장 구분하기 쉬운것은 막대 모양 그래프로, dfs를 끝까지 진행해봤을때 끝점이 존재하면(outdegree가 0인 정점이 존재하면) 막대 모양 그래프입니다.

이제 남은건 도넛 모양 그래프와 8자 모양 그래프인데,

둘 모두 사이클이지만 8자 모양 그래프는 outdegree가 2인 정점이 있습니다.

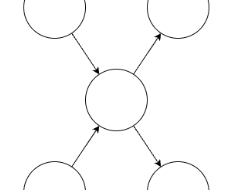
그리고 8자 모양 그래프의 경우 어떤 정점에서던지 dfs를 하면 반드시 outdegree가 2인 정점을 지나게 되기 때문에,

1. dfs를 진행하며
2. 끝을 만나면 막대 모양 그래프
3. outdegree가 2인 정점을 만나면 8자 모양 그래프
4. 아무것도 만나지 못하고 사이클임을 확인하면 도넛 모양 그래프

로 구분지어줄 수 있습니다.

전체 소스코드

전체 소스코드는 아래와 같습니다.

#include <bits/stdc++.h>
using namespace std;

int outdegree[1234567] = {0};
int indegree[1234567] = {0};
int vis[1234567] = {0};

vector<int> g[1234567]; // 인접리스트
vector<int> ans(4);

void dfs(int now){
    if(vis[now]){ ans[1]++; return; }
    if(outdegree[now] == 2){ ans[3]++; return; }
    if(outdegree[now] == 0){ ans[2]++; return; }
    vis[now] = 1;
    
    for(auto nxt : g[now]){
        dfs(nxt);
    }
}

vector<int> solution(vector<vector<int>> edges) {
    for(auto k : edges){
        outdegree[k[0]]++;
        indegree[k[1]]++;
        
        g[k[0]].push_back(k[1]);
    }
    
    for(int i=1; i<=1000000; i++){
        if(indegree[i] == 0 && outdegree[i] >= 2){ // 핵심 정점을 찾음.
            ans[0] = i;
            break;
        }
    }
    
    for(auto child : g[ans[0]]){
        dfs(child);
    }
    
    return ans;
}

첨언

indegree와 outdegree는 사실 위상정렬할때 주로 써먹는 개념이라서, 일반적인 그래프 문제에서 적용해서 풀어야 한다는게 좀 씽크빅이었던 문제.

indegree를 구하는 발상이 핵심인것 같고, outdegree 자체는 인접리스트를 만들고 나면 g[now].size() 로도 똑같이 구할 수 있기 때문에 크게 중요한 개념은 아닙니다.

그래프를 구분하는거 자체는 단순하게 dfs를 돌리면 되고, 백준으로 환산하자면 골드까지는 가지 않을까 싶습니다.