2024-04-24 • 7 min read

금광세그와 boj 16993

최근 ett/hld도 그렇고, 구간에 대해서 다루는 쿼리에 대해서 좀 깊게 공부해보고 있다. 일반적인 부분합 세그먼트 트리와는 다른 형태의 문제들을 해결해보고 있기에, 발상을 좀 정리해보고자 한다.

세그먼트 트리와 구간

세그먼트 트리의 주요 조건 및 세그트리가 주로 필요한 장소는

구간에 대한 쿼리를 진행하면서
각 쿼리당 처리시간이 빨라야 하고
인접한 두 구간이 서로 병합될 수 있어야 한다.

특히나 마지막 조건이 제일 중요한데, 기존의 구간합 세그먼트 트리나 Range Max Query 세그먼트 트리 등등 모두 인접한 두 구간을 병합할 수 있다는 특징이 있다.

이는 덧셈이나 최대/최소 등의 단순한 형태의 계산 뿐만 아니라 서로 merge 될 수 있다면 그 무엇이든 가능하며, 어떻게보면 segment tree와 비슷한 merge sort tree도 동일한 맥락에서 병합 가능하다는 특성을 공유하고 있다.

이러한 구간을 서로 합치는 아이디어를 차용해서 heavy-light decomposition이나 sqrt decomposition 등의 다양한 분할을 시도해보기도 하며, 결국 엄청나게 커서 계산할 수 없을 것 같은 구간을

더 작은 구간으로 분할해서 빠르게 해결하는것

이 세그를 시작으로 하는 구간 시리즈들의 핵심 발상인 것 같다.

boj 16993 연속합과 쿼리

이러한 두 구간의 병합을 묻는 응용 유형이 바로 그 말도많은 금광 세그 인 것인데, 금광 세그는 구간 [l,r] 내부에서 최대 부분합의 값을 찾아낼 수 있도록 해준다.

일반적인 덧셈 등의 연산으로는 최대 부분합을 저장하면서 서로 병합할 수 없기에, 구조체를 만들어서 관리하게 된다.

덧셈 연산자를 오버로딩해서 사용하면 편리하다

금광세그에서 요구하는 쿼리 문을 좀 더 명확하게 정의해보자면,

[L,R] 쿼리 구간 내부에서
L <= a < b <= R 인 [a,b]에 속하는 모든 값의 합을 K라 할 때,
이 K의 최댓값.

이 되는데, 이 문제를 세그먼트 트리로 해결하기 위해서는

서로 다른 구간 A와 B 사이의 병합을 통해 새로운 구간 C 을 만들어 내는 과정이 필요하다.

이때 구간을 병합하기 위한 핵심 아이디어는 구간C 내에서의
최대 부분합 구간 [a', b'] 에서의 a'와 b'를 각각 어느 구간이 가져가느냐 가 되는데,

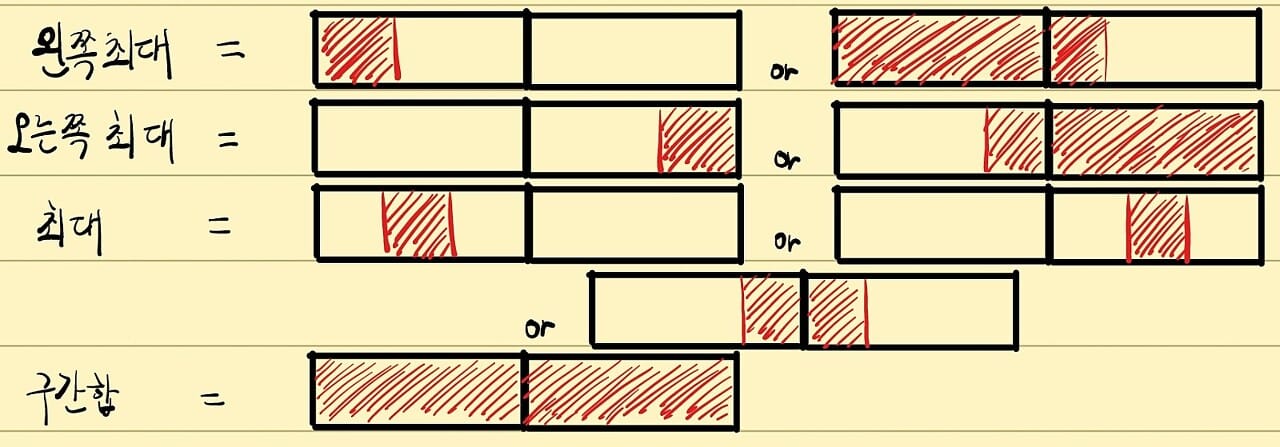
a'과 b'이 모두 왼쪽에 쏠린 경우
a'과 b'이 모두 오른쪽에 쏠린 경우
a'은 왼쪽이, b'은 오른쪽이 가져가는 경우 ( a' < b' 이므로 반대는 성립 불가능 )

이렇게 세가지로 쪼개볼 수 있다.

이런 측면에서 미리 저장해 두어야 할 값은,

기존 최대 부분합 구간
구간의 오른쪽 끝을 포함하는 최대 부분합 구간
구간의 왼쪽 끝을 포함하는 최대 부분합 구간
전체 구간에서의 부분합

이 네가지를 모두 가져가야 한다.

struct sec{
    ll all=0;
    ll left=0;
    ll right=0;
    ll mid=0;

    const sec operator+(const sec &K){
        sec ret;
        ret.all = all+K.all;
        ret.left = max(all+K.left, left);
        ret.right = max(right+K.all, K.right);
        ret.mid = max({mid, K.mid, right+K.left});
        return ret;
    }
};

이제 구현된 구조체를 볼 텐데, 오버로드된 연산자를 통한 두 구간의 병합 위주로 보겠다.

기존 구간을 왼쪽, 오른쪽 구간을 K로 받아와서 병합하는 예시이다.

all은 전체 구간에서의 합을 의미하기 때문에,
그냥 두 구간을 서로 더한다.
left는 왼쪽 끝을 포함하는 최대 부분합 구간인데,
왼쪽 끝부터 구간의 절반을 가로질러 오른쪽 구간까지 포함하는 경우 all + K.left,
왼쪽 끝에서 시작해 왼쪽 구간에서 끝나는 경우 left
이므로 둘 중 최댓값을 선택한다.
right 역시
[왼쪽 구간 ~ 구간의 경계선 ~ 오른쪽 끝] 인 경우 right+K.all,
[오른쪽 구간 ~ 오른쪽 끝] 인 경우 K.right
이므로 둘 중 최댓값을 선택하고,
mid는 구간의 중간에서 시작해 중간에서 끝나는 경우인데
각 구간에서의 최대 부분합 구간 mid와 K.mid,
두 구간이 합쳐서 새로 생기는 부분합 구간 right+K.left
사이의 최댓값으로 갱신해주면 된다.

다른 분의 블로그에서 굉장히 직관적으로 설명해주고 있기에, 사진을 첨부한다.

이렇게 두 구간을 병합할 수 있으면 병합된 한 구간에서 새로운 4개의 값을 가지게 되는데, 이들 중 최대 부분합이 존재하므로

정답에서 출력하고자 할 때에

cout << max({ret.all, ret.left, ret.right, ret.mid}) << "\n";

위와 같이 출력해주면 된다.

금광세그를 활용한 문제들

이제 주어지는 쿼리 [s,e] 구간을 빠르게 병합할 수 있는
segment tree를 도입하면 이 문제를 해결할 수 있으며,

각 좌표에 대한 좌표압축을 진행한 뒤
두 y좌표 [y1,y2] 를 O(N^2) 에 선택하고
구간 내의 점들을 segment tree에 넣어서
최대 부분합을 구하는 boj 10167 금광 문제가 존재하고,

추가적으로 트리상에서의 경로 [u,v] 에서 동일한 쿼리를
euler tour technique + heavy-light decomposition + segment tree
조합으로 해결해야 하는 boj 13519 - 트리와 쿼리 10 문제가 존재한다.